Kleene's O
In set theory and computability theory, Kleene's  is a canonical subset of the natural numbers when regarded as ordinal notations. It contains ordinal notations for every recursive ordinal, that is, ordinals below Church–Kleene ordinal,
is a canonical subset of the natural numbers when regarded as ordinal notations. It contains ordinal notations for every recursive ordinal, that is, ordinals below Church–Kleene ordinal, 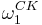 . Since
. Since 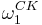 is the first ordinal not representable in a computable system of ordinal notations the elements of
is the first ordinal not representable in a computable system of ordinal notations the elements of  can be regarded as the canonical ordinal notations.
can be regarded as the canonical ordinal notations.
Kleene (1938) described a system of notation for all recursive ordinals (those less than the Church–Kleene ordinal). It uses a subset of the natural numbers instead of finite strings of symbols. Unfortunately, there is in general no effective way to tell whether some natural number represents an ordinal, or whether two numbers represent the same ordinal. However, one can effectively find notations which represent the ordinal sum, product, and power (see ordinal arithmetic) of any two given notations in Kleene's  ; and given any notation for an ordinal, there is a recursively enumerable set of notations which contains one element for each smaller ordinal and is effectively ordered.
; and given any notation for an ordinal, there is a recursively enumerable set of notations which contains one element for each smaller ordinal and is effectively ordered.
Contents |
Kleene's 
The basic idea of Kleene's system of ordinal notations is to build up ordinals in an effective manner. For members  of
of  , the ordinal for which
, the ordinal for which  is a notation is
is a notation is 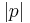 . The standard definition proceeds via transfinite induction and the ordering
. The standard definition proceeds via transfinite induction and the ordering  (a partial ordering of Kleene's
(a partial ordering of Kleene's  ) is defined simultaneously.
) is defined simultaneously.
- The natural number 0 belongs to Kleene's
 and
and 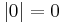 .
. - If
 belongs to Kleene's
belongs to Kleene's  and
and  , then
, then 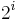 belongs to Kleene's
belongs to Kleene's  and
and 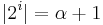 and
and 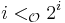 .
. - Suppose
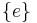 is the
is the  -th partial recursive function. If
-th partial recursive function. If  is total, with range contained in
is total, with range contained in  , and for every natural number
, and for every natural number  , we have
, we have 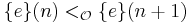 , then
, then 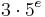 belongs to Kleene's
belongs to Kleene's  ,
, 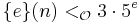 for each
for each  and
and 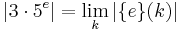 , i.e.
, i.e. 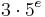 is a notation for the limit of the ordinals
is a notation for the limit of the ordinals 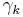 where
where 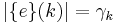 for every natural number
for every natural number  .
. 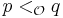 and
and 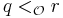 imply
imply 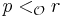 (this guarantees that
(this guarantees that 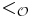 is transitive.)
is transitive.)
This definition has the advantages that one can recursively enumerate the predecessors of a given ordinal (though not in the 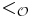 ordering) and that the notations are downward closed, i.e., if there is a notation for
ordering) and that the notations are downward closed, i.e., if there is a notation for  and
and 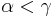 then there is a notation for
then there is a notation for  .
.
Basic properties of 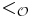
- If
 and
and  and
and 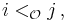 then
then 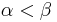 ; but the converse may fail to hold.
; but the converse may fail to hold. 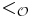 induces a tree structure on
induces a tree structure on  , so
, so  is well-founded.
is well-founded. only branches at limit ordinals; and at each notation of a limit ordinal,
only branches at limit ordinals; and at each notation of a limit ordinal,  is infinitely branching.
is infinitely branching.- Since every recursive function has countably many indices, each infinite ordinal receives countably many notations; the finite ordinals have unique notations,
 usually denoted
usually denoted 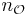 .
. - The first ordinal that doesn't receive a notation is called the Church–Kleene ordinal and is denoted by
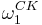 . Since there are only countably many recursive functions, the ordinal
. Since there are only countably many recursive functions, the ordinal 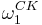 is evidently countable.
is evidently countable. - The ordinals with a notation in Kleene's
 are exactly the recursive ordinals. (The fact that every recursive ordinal has a notation follows from the closure of this system of ordinal notations under successor and effective limits.)
are exactly the recursive ordinals. (The fact that every recursive ordinal has a notation follows from the closure of this system of ordinal notations under successor and effective limits.) 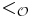 is not recursively enumerable, but there is a recursively enumerable relation which agrees with
is not recursively enumerable, but there is a recursively enumerable relation which agrees with 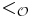 precisely on members of
precisely on members of  .
.- For any notation
 , the set
, the set 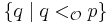 of notations below
of notations below  is recursively enumerable. However, Kleene's
is recursively enumerable. However, Kleene's  , when taken as a whole, is
, when taken as a whole, is 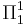 (see analytical hierarchy).
(see analytical hierarchy). - In fact,
 is
is 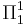 -complete and every
-complete and every 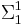 subset of
subset of  is effectively bounded in
is effectively bounded in  (a result of Spector).
(a result of Spector).  is the universal system of ordinal notations in the sense that any specific set of ordinal notations can be mapped into it in a straightforward way. More precisely, there is a recursive function
is the universal system of ordinal notations in the sense that any specific set of ordinal notations can be mapped into it in a straightforward way. More precisely, there is a recursive function  such that if
such that if  is an index for a recursive well-ordering, then
is an index for a recursive well-ordering, then 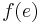 is a member of
is a member of  and
and 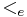 is order-isomorphic to an initial segment of the set
is order-isomorphic to an initial segment of the set 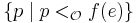 .
.- There is a recursive function
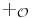 , which, for members of
, which, for members of  , mimics ordinal addition and has the property that
, mimics ordinal addition and has the property that 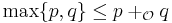 . (Jockusch)
. (Jockusch)
Properties of paths in 
A path in  is a subset
is a subset 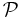 of
of  which is totally ordered by
which is totally ordered by 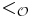 and is closed under predecessors, i.e. if
and is closed under predecessors, i.e. if  is a member of a path
is a member of a path 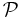 and
and 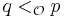 then
then  is also a member of
is also a member of 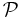 . A path
. A path 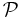 is maximal if there is no element of
is maximal if there is no element of  which is above (in the sense of
which is above (in the sense of 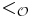 ) every member of
) every member of 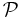 , otherwise
, otherwise 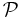 is non-maximal.
is non-maximal.
- A path
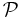 is non-maximal if and only if
is non-maximal if and only if 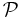 is recursively enumerable (r.e.). It follows by remarks above that every element
is recursively enumerable (r.e.). It follows by remarks above that every element  of
of  determines a non-maximal path
determines a non-maximal path 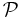 ; and every non-maximal path is so determined.
; and every non-maximal path is so determined. - There are
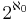 maximal paths through
maximal paths through  ; since they are maximal, they are non-r.e.
; since they are maximal, they are non-r.e. - In fact, there are
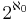 maximal paths within
maximal paths within  of length
of length 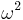 . (Crossley, Shutte)
. (Crossley, Shutte) - For every non-zero ordinal
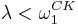 , there are
, there are 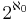 maximal paths within
maximal paths within  of length
of length 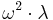 . (Aczel)
. (Aczel) - Further, if
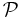 is a path whose length is not a multiple of
is a path whose length is not a multiple of 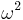 then
then 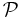 is not maximal. (Aczel)
is not maximal. (Aczel) - For each r.e. degree
 , there is a member
, there is a member 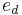 of
of  such that the path
such that the path 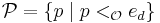 has many-one degree
has many-one degree  . In fact, for each recursive ordinal
. In fact, for each recursive ordinal 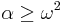 , a notation
, a notation 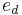 exists with
exists with 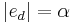 . (Jockusch)
. (Jockusch) - There exist
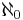 paths through
paths through  which are
which are 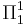 . Given a progression of recursively enumerable theories based on iterating Uniform Reflection, each such path is incomplete with respect to the set of true
. Given a progression of recursively enumerable theories based on iterating Uniform Reflection, each such path is incomplete with respect to the set of true 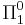 sentences. (Feferman & Spector)
sentences. (Feferman & Spector) - There exist
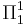 paths through
paths through  each initial segment of which is not merely r.e., but recursive. (Jockusch)
each initial segment of which is not merely r.e., but recursive. (Jockusch) - Various other paths in
 have been shown to exist, each with specific kinds of reducibility properties. (See references below)
have been shown to exist, each with specific kinds of reducibility properties. (See references below)
See also
References
- Church, Alonzo (1938), "The constructive second number class", Bull. Amer. Math. Soc. 44 (4): 224–232, doi:10.1090/S0002-9904-1938-06720-1, http://www.ams.org/bull/1938-44-04/S0002-9904-1938-06720-1/
- Kleene, S. C. (1938), "On Notation for Ordinal Numbers", The Journal of Symbolic Logic (Association for Symbolic Logic) 3 (4): 150–155, doi:10.2307/2267778, JSTOR 2267778
- Rogers, Hartley (1987) [1967], The Theory of Recursive Functions and Effective Computability, First MIT press paperback edition, ISBN 978-0-262-68052-3
- Feferman, Solomon; Spector, Clifford (1962), "Incompleteness along paths in progressions of theories", Journal of Symbolic Logic 27 (4): 383–390, doi:10.2307/2964544